De reeks van Fibonacci

Leonardo van Pisa, beter bekend als Fibonacci, geboren in Italië rond 1175,
is de bedenker van de Fibonacci reeks.

De reeks van Fibonacci is een reeks van getallen waarbij elk getal gelijk is aan de som van de twee voorgaande getallen; F(n)=F(n-1)+F(n+2)

dus;
0 + 1 = 1
1 + 1 = 2
2 + 1 = 3
3 + 2 = 5
5 + 3 = 8
etc..

De oudste bron waarin het werk van Fibonacci wordt besproken is een monoloog van Kepler in 1611.
Kepler was niet op de hoogte van Fibonacci's werk en herontdekte de reeks.
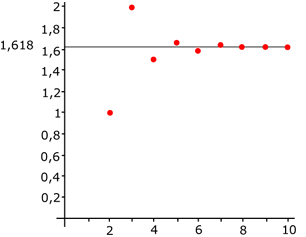
Hij deed een ontdekking over de verhoudingen tussen de op elkaar volgende getallen, deze naderen de waarde 1.618.
Hij noemde het de goddelijke verhouding, wat wij tegenwoordig de gulden snede noemen.

De rij van Fibonacci is terug te vinden in de natuur maar ook in de kunst, muziek en architectuur.

de groei van een boom komt overeen met de rij van Fibonacci

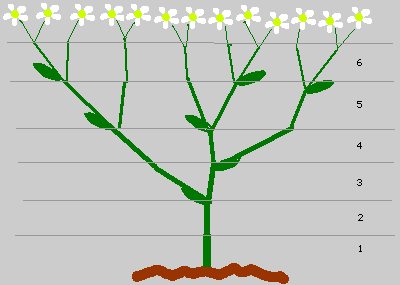
de groei schematisch verbeeld.

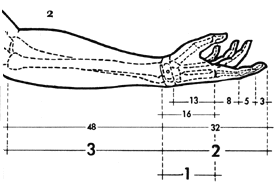
de afmetingen van de botten in een arm volgen de reeks van Fibonacci

13 noten scheiden elk octaaf van 8 noten in een toonladder,
waarvan de 5de en 3de noten de ondergrond vormen van alle akkoorden,
en zijn gebaseerd op hele tonen die 2 stappen van de hoofdtoon verwijderd ligt,
die de 1ste noot is van de toonladder.
Ook is de piano verdeeld in 13 toetsen, waarvan er 8 wit zijn en 5 zwart, gegroepeerd in sets van 3 en 2.

de groei van een blad volgt Fibonacci

de groei van een denneappel volgt Fibonacci

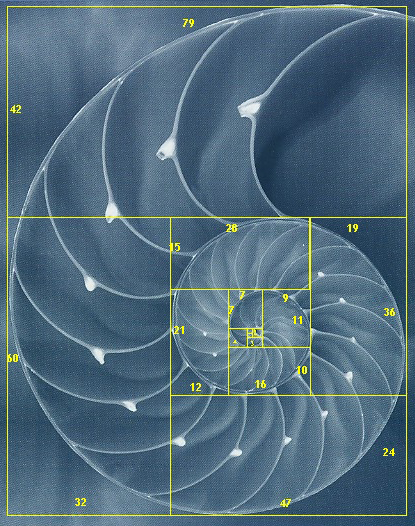
de groei van een slak volgt Fibonacci

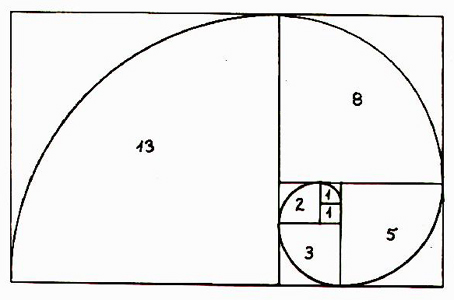
een vierkant opgebouwd volgt Fibonacci

artikel NRC

zie ook Hans Bär

naar boven ↑